نکات قابل توجه برای زندگی روشن

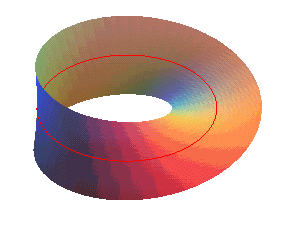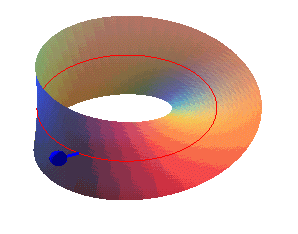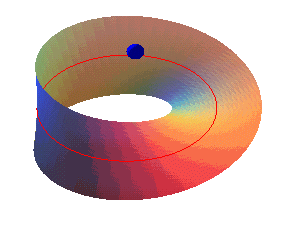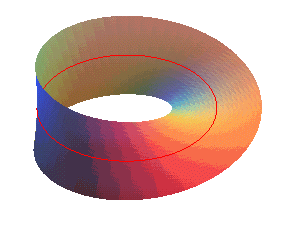
گفتنی است:پزشکان توصیه می کنند تا افراد برای عدم کاهش تمرکز و حواس سعی کنند تا از خوردن غذاهای سنگین و چرب و بویژه لبنیات مانند دوغ قبل از تشکیل کلاس خودداری کنند و از غذاهای سبک اما مقوی که قابلیت هضم سریع دارند استفاده کنند.

بررسی ها نشان می دهند: عوامل متعددی بر کاهش یا افزایش تمرکز دانش آموزان تاثیر گذار است از جمله تهویه ی مناسب کلاس و دمای هوا، میزان نور کافی در فضای کلاس، نوع صندلی و ارتفاع آن و همینطور فاصله ی دانش آموز از جلوی کلاس و تخته سیاه یا سفید همگی می تواند مؤثر باشد.

روانشناسان توصیه می کنند: تا افراد برای افزایش تمرکز سعی کنند از لباس های راحت و کفش های مناسب استفاده کنند و درصورتی که برایشان امکان پذیر است قبل از شروع کلاس پیش خوانی انجام دهند تا میزان انرژی کمتری را برای درک مطالب صرف کنند.

از جمله موارد دیگر عدم استفاده از مواد خوشبو کننده ی بدن مانند انواع عطرها و اسپری ها می باشد زیرا می تواند باعث بروز سردرد و میگرن در فرد شود.

مصرف مایعات فراوان نیز می تواند به افزایش تمرکز فرد کمک کند.

استفاده از روش‌های تشویقی برای ترغیب کودک به گفتن حقیقت و اعتراف به کار اشتباهش موثرتر از تنبیه است.

به گزارش سرویس اجتماعی خبرگزاری دانشجویان ایران (ایسنا)، کارشناسان علوم رفتاری کودکان می‌گویند: اطمینان از تنبیه نشدن، انگیزه دروغگویی را از کودک می‌گیرد.

کودکان همراه با رشد شناختی و اجتماعی، دروغ گفتن را از اطرافیان و همسالانشان یاد می‌گیرند. شروع این مساله معمولا از سن 2 سالگی آغاز می‌شود. اولین دروغ کودکان معمولا برای انکار کارهای اشتباهشان است. از سن 3 سالگی، کودکان شروع به گفتن دروغ‌های مصلحتی می‌کنند.

دروغ گفتن آنها در دوران پیش از مدرسه و در مهدکودک بیشتر می‌شود چرا که آنها نسبت به احساس و تفکرات دیگران آگاهی بیشتری به دست می‌آورند و زمان‌هایی را که برای دروغ مناسب می‌دانند انتخاب می‌کنند و هرچه بزرگ‌تر می‌شوند یاد می‌گیرند که دروغ‌های قانع‌کننده‌تری بگویند اما این کار به مراتب برای آنها سخت‌تر می‌شود به خصوص زمانی که سوالات بیشتری از آنها پرسیده شود.

به گزارش ایسنا به نقل از گاردین، بررسی‌ها نشان داده نوجوانانی که مهارت‌های اجتماعی ضعیفی دارند قادر به گفتن دروغ‌های متقاعدکننده نیستند. همچنین کودکانی که اغلب دروغ می‌گویند پرخاشگرتر از همسالان خود هستند و رفتارهای متناقض بیشتری دارند.

کارشناسان با بررسی کودکان 4 تا 8 ساله به این نتیجه رسیدند که می‌توان با روش‌های خاصی کودکان را تشویق به گفتن حقیقت کرد. کارشناسان در این مطالعه تاکید کردند در صورتی که می‌خواهید فرزندتان حقیقت را بگوید و به اشتباهش اعتراف کند، باید او را از اینکه تنبیهی در انتظارش نخواهد بود مطمئن کنید. همچنین اگر از جملات تشویقی استفاده کنید و مثلا به کودک بگویید که اگر حقیقت را بگوید، شما را بسیار خوشحال خواهد کرد، او خیلی بیشتر به گفتن حقیقت راغب می‌شود.

نگها با تمامی عوامل و جزئیات زندگی ما چنان رابطه تنگاتنگی دارند که باید گفت رنگها بسان پله هایی هستند که وجود فیزیکی و روحی انسانها را با سایر جزئیات و پدیده های جهان هستی در ارتباط قرار می دهند این ارتباط و تاثیر به حدی است که حتی انسانها در کلمات و جملات خود نیز برای بیان احساسات درونیشان از رنگها استفاده کرده و آن را بیان می دارند.
 
1.برای لاغر شدن ، از بشقاب و رومیزی آبی رنگ استفاده کنید. رنگ آبی اشتها را کم می‌کند
 
2.اگر کم خواب هستید وسایل اتاق خواب را به رنگ بنفش درآورید یا از چراغ خواب به رنگ بنفش استفاده کنید. رنگ بنفش آرامش دهنده و خواب‌آور است.
  
3.اگر از کم خونی رنج می‌برید، میوه‌های قرمز رنگ مانند گیلاس ، توت فرنگی و گوشت قرمز مصرف کنید.  

4.اگر بی‌حال و حوصله هستید، رنگ نارنجی را انتخاب کنید، هنگام استحمام صبحگاهی از حوله و ابزار نارنجی استفاده کنید، رنگ نارنجی. بی‌حالی شما را از بین می‌برد  
 
5.اگر مشکلی پیش روی شماست، از رنگ نیلی استفاده کنید، رنگ نیلی کمک می‌کند تا بهتر بیندیشید .

6.اگر مضطرب هستید و فشار عصبی طاقت شما را بریده است، از رنگ سبز استفاده کنید. رنگ سبز آرامبخش است و فشار خون را کاهش می‌دهد.
  
7.افراد افسرده لباس زرد رنگ بپوشند. غذاهای زرد بخورند و رنگ زرد را اطراف خود بجویند. رنگ زرد سطح انرژی را بالا برده و مانع افسردگی می‌شود.

ریاضیات پر از شگفتی است. این شگفتی ها بیشتر حاصل همخوانی نظریات مجردریاضی با طبیعت عینی و ملموس پیرامون ماست.
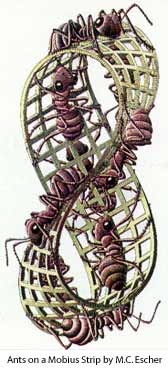
نوار موبیوس یکی از هزاران موضوع جالبی است که هم از لحاظ نظری و هم از لحاظهندسی جذابیت های ویژه ای برای ریاضیدانان دارد.

آگوست فردیناند موبیوس (August Ferdinand Möbius) در روز 17 نوامبر 1790 در شهر زاکسن به دنیا آمد. وی ریاضیدان و ستاره شناس مشهور آلمانی است. بیشتر شهرت او به دلیل کشف نوار موبیوس است.

نوار موبیوس نواری است که دو لبه آن بر هم قرار گرفته و حلقه‌ای را به وجود می‌آورد؛ البته باید یک لبه انتهایی قبل از اتصال به لبه دیگر نیم دور چرخانده شود. این نوار را دوریاضیدان آلمانی به نامهای آگوست فردیناند موبیوس و جان بندیکت (Johann Benedict) در سال 1858 به طور مستقل و جداگانه کشف کردند و به ثبت رساندند.

اتما گاندی نیازی به معرفی ندارد. همه، مردی را که رهبری ملت هند را برای استقلال از سلطه انگلیس در سال 1947 بر عهده داشت می‌شناسند.

خودتان را تغییر دهید

شما باید مظهر تغییری باشید که می‌خواهید در جهان ببینید. اگر خود را تغییر دهید، جهان خود را نیز تغییر می‌دهید. اگر شیوه تفکرتان را تغییر دهید، می‌توانید احساسات و اعمالتان را تغییر دهید و بنابراین جهان اطراف شما نیز تغییر می‌کند، نه  تنها به این دلیل که اکنون شما اطرافتان را با فکر و احساسات تازه‌ای می‌نگرید، بلکه به این دلیل که این تغییر می‌تواند به شما کمک کند تا دست به عمل بزنید، به شیوه ای که قبلاً فکر آن را نمی‌کردید ولی غرق در الگوهای فکری قدیمی خود بودید.

شما تحت کنترل هستید

شما می‌توانید اندیشه‌ها، واکنش‌ها یا احساساتتان را تقریباً در مورد هر چیزی انتخاب کنید.

نباید هیجان زده شوید، رفتار اغراق آمیزی انجام دهید یا به صورت منفی واکنش نشان دهید. البته ممکن است همیشه و بلافاصله این‌گونه نباشد. بعضی اوقات یک حرکت بدون تفکر انجام می‌شود. یا یک تفکر کهنه نمایان می‌گردد. وقتی بفهمید که هیچ چیز بیرونی نمی‌تواند احساس شما را کنترل کند، می‌توانید به تدریج این اندیشه را به زندگی روزانه خود وارد و آن را تبدیل به یک عادت کنید.   عادتی که می‌تواند به مرور زمان قوی‌تر و قوی‌تر شود. با این کار زندگی بسیار آسان‌تر و دلپذیرتر می‌گردد.

ببخشید و رها کنید

شخص ضعیف هرگز نمی‌بخشد. عفو و بخشش نشانه قدرت است. جنگ با بدی با روش اشتباه به هیچ کس کمکی نمی‌کند؛ و همان طور که در نکته قبلی گفته شد، این شمایید که انتخاب می‌کنید چگونه واکنشی نشان دهید. وقتی این تفکر را هر چه بیشتر وارد زندگی‌تان کنید، می‌توانید به طریقی دست به عمل بزنید که برای خودتان و دیگران مفید باشد. شما می‌فهمید که بخشش و رها کردن گذشته باعث کمک به شما و مردم جهانتان می‌شود.

بدون عمل به جایی نمی‌رسید

یک مثقال عمل بهتر است از یک خروار حرف. ممکن است فقط حرف بزنید. یا به صورت بی پایان درس بخوانید و مطالعه کنید؛ و فکر کنید که به سمت جلو در حرکتید. اما در زندگی واقعی نتایج کمی کسب کرده باشید.

به این لحظه توجه کنید

چرا؟ زیرا زمانی که شما در زمان حال به سر می‌برید، در مورد لحظات بعدی که تحت کنترل شما نیستند، نگرانی ندارید؛ و این مقاومت که از انجام هرگونه عملی جلوگیری می‌کند، قدرتش را در نتیجه تصور نتایج منفی در آینده از دست می‌دهد؛  و بنابراین راحت‌تر می‌توانیم هم وارد عمل شویم و هم بر زمان حاضر تمرکز کنیم و بهتر عمل کنیم. همه انسانیم  وقتی شروع به اسطوره ساختن از افراد کنید، این خطر وجود دارد که دیگر نتوانید با آن‌ها ارتباط برقرار کنید. ممکن است کم کم فکر کنید که شما هرگز نمی‌توانید به چیزهای مشابه آن‌ها دست یابید، زیرا آن‌ها خیلی متفاوت هستند. بنابراین مهم است که به یاد داشته باشید همه ما گذشته از اینکه چه کسی هستیم، انسانیم.

پایداری

پایدار و محکم باشید. در آینده مخالفت‌های اطرافتان کمرنگ و نابود می‌شود؛ و مقاومت درونی شما و خود تخریبی که می‌خواهد شما را عقب نگه دارد و از پیشرفت‌تان جلوگیری کند، روز به روز ضعیف‌تر می‌شوند. موفقیت و پیروزی به ندرت با آن سرعتی که می‌خواهید به دست می‌آید. یکی از دلایلی که افراد به آنچه که می‌خواهند نمی‌رسند، این است که
آن‌ها خیلی زود خسته می‌شوند.

خوبی مردم را ببینید و به آن‌ها کمک کنید

من فقط به جنبه‌های خوب انسان‌ها توجه می‌کنم. از آنجایی که خودم بی عیب و نقص نیستم، علاقه‌ای به کشف خطاهای دیگران ندارم. بیشتر وقت‌ها، افراد ویژگی‌های خوبی دارند و همچنین ممکن است بعضی ویژگی‌هایشان چندان خوب نباشد. اما شما می‌توانید تصمیم بگیرید که به کدام توجه کنید. اگر به دنبال پیشرفت هستید، روی خوبی افراد تمرکز کنید. این کار باعث می‌شود که زندگی برای شما آسان‌تر شود همزمان که دنیا و روابطتان مثبت‌تر و دلپذیرتر می‌شود. زمانی که شما خوبی افراد را می‌بینید، کمک کردن به آن‌ها برای شما راحت‌تر می‌شود.

هماهنگ و قابل اعتماد باشید

خود واقعی‌تان باشید و تظاهر نکنید. همیشه بین اندیشه، گفتار و کردارتان هماهنگی ایجاد کنید. یکی از بهترین نکات برای بهبود مهارت‌های اجتماعی، رفتار یکسان و ارتباط براساس اعتماد است. به نظر می‌رسد افراد واقعاً به ارتباط درست و اطمینان بخش علاقه دارند؛ و زمانی که اندیشه، گفتار و کردار شما در یک راستا باشد، به لذت درونی بالایی می‌رسید.

رشد کنید و به تعالی برسید

پیشرفت مداوم، قانون زندگی است. شما همیشه می‌توانید توانایی‌ها و عادت‌هایتان را بهبود ببخشید و خود را مجدداً مورد ارزیابی قرار دهید. شما می‌توانید درک عمیق‌تری از خود و جهانتان بدست آورید.

جورج پولیا: ریاضیات عبارت است از اثبات بدیهی ترین چیز به نابدیهی ترین روش ممکن.

پواسون: زندگانی تنها به این درد می خورد که انسان به دو کار مشغول گردد: اول: ریاضی بخواند، دوم: ریاضی درس بدهد.

کیلی: درهر چیز از جمله یک نظریه ریاضی زیبایی را میتوان درک کرد اما نمی توان توضیح داد.

ایمانوئل کانت: علم ریاضی درخشان ترین مثال برای این واقعیت است که چگونه استدلال محض دامنه تاثیرگذاریش را بدون کمک تجربه گسترش می دهد.

پیرفرما: و شاید آیندگان از اینکه نشان داده ام قدیمی ها همه چیز را نمی دانستند، سپاسگزارمن باشند.

جان لاک: اثبات ریاضی مانند الماس قاطع و شفاف است، و با چیزی جز استدلال دقیق نمی توان به آن رسید.

دمورگن: نیروی محرکه ابداع ریاضی استدلال نیست، تخیل است.

د.یا. سترویک: باید به یاد داشته باشید که مفهوم های ریاضی نتیجه ای از کار آزاد ذهن نیستند بلکه انعکاسی از جهان واقعی و عینی دور وبر ما هستند که البته اغلب به صورت کاملا انتزاعی طرح می شود.

ب.فلدلیوم: هر کشف تازه ای که در علوم طبیعی و صنعت رخ میدهد تنها از راه به کار بردن نتیجه گیری های جدید در عمل و یا زنده کردن نظریه های فراموش شده ریاضی است به این ترتیب نظریه های ریاضی از قبل راه پیشرفت علم وصنعت را پیش بینی می کنند.

هیلبرت: با وجود اهمیتی که کاربرد ریاضیات دارد اما این کار نباید ملاک ارزش گذاری آن باشد. 
جینز: به نظر میرسد معمار بزرگ جهان ریاضیدان است. 
برتراند راسل: ریاضیات هیچ حقیقتی ندارد اما بالاترین زیبایی را داراست . یک زیبایی سرد و جدی، درست مانند یک تندیس ، به طور شگفت انگیزی محض ، و توانا در نهایت جدیت، به طوری که تنها بزرگترین هنرمندان می توانند این گونه باشند.

گاوس: ریاضیات حاکم علوم است و نظریه اعداد ملکه ریاضیات.

فیثاغورس: بدون ریاضیات شاید هنر و ادبیات داشته باشیم ولی تکنولوژی و صنعت هرگز چیزی در جهان وجود ندارد که با عدد قابل بیان نباشد.

فیثاغورس: به کمک اعداد می توان زندگی و پیشامد های آن را پیش بینی کرد.

هانری پوانکاره: دانشمند، طبیعت را به خاطر فایده اش مطالعه نمی کند، آن را برای این مطالعه می کند که از آن لذت می برد و چون طبیعت زیباست از آن لذت می برد. اگر طبیعت زیبا نبود، ارزش شناختن نداشت و اگر طبیعت ارزش شناختن نداشت، زندگی هم ارزش زیستن نداشت . البته، من دراینجا از آن گونه زیبایی که حواس را متأثر می کند، یعنی از زیبایی اوصاف و ظواهر، سخن نمی گویم؛ نه به این جهت که این زیبایی ها را دست کم بگیرم، نه چنین نیست، اما این زیبایی ربطی به علوم ندارد، منظورم زیبایی ژرف تری است که از نظم هماهنگ اجزا بوجود می آید و تنها هوش ناب قادر به درک آن است.

فیثاغورس: به کمک اعداد می توان زندگی و پیشامد های آن را پیش بینی کرد.

گئورگ لیختن برگ: آنچه شما را به کشف کردن وا داشته است، کوره راهی در  شما می گشاید که، باز هم، هر وقت به چنین ضرورتی برخورد کنید میتوانید از ان استفاده کنید.

امانوئل کانت: هرگونه معرفت انسانی ازتفکر و تامل آغاز می شود، از آنها به  مفهم می رسد و سرانجام، به اندیشه ختم می شود.

ایای شور: استدلال غیر ریاضی نقش اساسی در استدلال های ریاضی دارد.

دکارت: هر راه حلی که برای مساله ای پیدا می کنم به عنوان سر مشق به من کمک می کند تا مساله های دیگر را هم به نتیجه برسانم.

دیوید هیلبرت: اعتقاد به قابل حل بودن هر مساله ریاضی یک عامل محرک قوی برای کسی است که روی آن کار می کند. دردرون ما همیشه صدایی طنین انداز است که مساله ای پیش رو است برای حل آن تلاشت را به کار ببند. شما می توانید آن را با استدلال روشنی بیابید. در ریاضیات احساس عجز و ناامیدی جایی ندارد.

پاسکال: انسان تنها یک نی است، شکننده ترین در طبیعت؛ اما یک نی اندیشمند، لازم نیست که تمام جهان مسلح شود تا او را در هم شکند، یک بخار یک قطره آب برای کشتن او کافی است. اما هنگامی که جهان او را در هم می‌شکند، انسان باز هم والاتر از آن چیزی است که او را می‌کشد،  زیرا او می‌داند که می‌میرد و برتریی که جهان بر او دارد،  جهان از آن هیچ نمی‌داند.

پوانکاره: نام دانشمند به خصوص ریاضیدان را باید به کسی داد که در کار خود  به احساس یک هنرمند برسد و به اندازه یک هنرمند از محصول کار خود لذت  ببرد.

نیوتن: نمی‌دانم که در چشم جهان چگونه بوده ام. ولی در چشم خودم به نظر می‌رسد تنها همچون کودکی بازی کنان برکرانه دریا بوده ام و خود را با گهگاه یافتن ریگی نرم تر یا صدفی زیباتر از معمول سرگرم کرده ام در حالی که اقیانوس عظیم حقیقت نامکشوف در پیش روی من گسترده است.

ویلیام دبلیوسایر: امروزه شهرت ریاضی شبیهشهرت خودروی سواری در 50  سال پیش است در آن موقع تصور عمومی بر آن بود که خودروهاگران قیمت وخطرناکند وهیچ کس به جز یک مرد ثروتمند توانایی داشتن یک خودرورانداردیاهیچ کس به جزیک راننده حرفه ای نمی تواند رانندگی کند به  همین ترتیب هنوزباورعمومی ان است که ریاضی برای افراد استثنایی ،برای اجتماع نخبگان وبرای تعداد اندکیاست. الان زمان آن رسیده است که کسی برای ریاضی همان کار را بکند که فورد با ساختن مدل تی برای خودروهای سواری انجام داد و آنها رابه تولید انبوه رساند.

فلاطون :ریاضیات روح را صفا می بخشد و ذهن را برای درک حقیقت آماده می کند . غفلت از ریاضیات به تمام علوم و دانش ها لطمه می زند .

داوینچی :هیچ دانشی را نمی توان واقعی دانست مگر اینکه به صورت ریاضی نوشته شود.

پیر سیمون لاپلاس:تمام آثار طبیعت نتایج ریاضی چند قانون تفسیر ناپذیرند .

ژرژ کانتور:جوهر ریاضی در آزادی آن نهفته است این علم فارغ از تمام سیاست های جهان به توسعه خود ادامه می دهد و برخلاف سایر موارد توسعه با اقبال جهانی مواجه شده است .

آلبرت انیشتین:نگران مشکلاتی که در ریاضی دارید نباشید . به شما اطمینان می‌دهم که مشکلات من در این زمینه عظیم‌تر است .

افلاطون: خداوند در کار ریاضی است .

گالیله:قوانین طبیعت به زبان ریاضیات نوشته شده است .

آلبرت انیشتین: از وقتی که ریاضی‌دانان از سر و کول « نظریه نسبیت » بالا رفته‌اند، دیگر خودم هم از آن سر در نمی‌آورم .

آلبرت انیشتین:در دنیا خط مستقیم وجود ندارد و تمام خطوط بدون استثنا منحنی و دایره وار است و اگر این خط کوچکی که در نظر ما مستقیم جلوه می کند در فضا امتداد یابد خواهیم دید که منحنی است .

خیام:جبرها حقایق هندسی هستند که اثبات می شوند .

افلاطون: خداوند همیشه با قواعد هندسی تدبیر می کند .

هیلبرت:یک نظریه ی ریاضی را نمی توان کامل شمرد تا این که شما آن را به اندازه ای واضح سازید به طوری که بتوانید آن را برای اولین فردی که در خیابان با وی برخورد می کنید ، توضیح دهید .

گالیله: در ریاضیات آنچه مهم است، فکر کردن است ! ریاضیات الفبایی است که خداوند جهان را بر مبنای آن خلق کرد .

ژاکوب ژاکوبی:ذات حق همیشه به کار حساب مشغول است . /

عجیب‌ترین جمله در زبان انگلیسی!!!

این جمله با کلمه ای یک حرفی آغاز می شود? کلمه دوم دو حرفی است?‌ سوم سه حرفی، چهارم چهار حرفی تا بیستمین کلمه بیست حرفی:

I do not know where family doctors acquired illegibly perplexing handwriting nevertheless, extraordinary pharmaceutical intellectuality counterbalancing indecipherability, transcendentalizes intercommunications incomprehensibleness

ترجمه ی جمله :
نمیدانم این دکترهای خانوادگی این دست خطهای گیج کننده را از کجا کسب می کنند. با این حال سواد پزشکی انها غیر قابل کشف بودن این دست خط ها را جبران کرده است.

فرض کن حضرت مهدی به تو ظاهر گردد

    ظاهرت هست چنانی که خجالت نکشی؟

         باطنت هست پسندیده ی صاحب نظری؟

              خانه ات لایق او هست که مهمان  گردد؟

                    لقمه ات در خور او هست که نزدش ببری؟

                         پول  بی شبهه و سالم  ز هــمه داراییــت

                               داری آن قدر که یک هدیه برایش بخری ؟

                                     حاضری گوشی همراه تو  را چک بکند؟

                                           با چنین شرط که درحافظه دستی نبری؟

                                                 واقفی بر عمل خویش تو بیش از دگران

                                                       می توان گفت تو را شیعه اثنی عشری؟

به امید روزی که در برگه تقویم خواهند نگاشت:

تعطیل رسمی " روز ظهور حضرت ولی عصر (عج) "